Skip to main content
Logo image

Quantum Computing: A gentle introduction for Liberal Arts Institutions

Levi Goldberg, Shun Suzuki, Javier Orduz

Section 2.2 Gates

Subsection 2.2.1 Hadamard gate

Hadamard gate is one of the most popular gates in quantum computing.
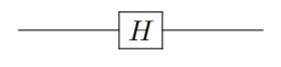
Figure 2.2.1. Hadamard gate representation in a circuit.
\begin{align} H=\frac{1}{\sqrt{2}} \begin{pmatrix} 1&1\\ 1&-1 \end{pmatrix}\tag{2.2.1} \end{align}
The Hadamard operator on one qubit can be written as
\begin{gather} H =\frac{1}{\sqrt{2}} \bigg( \Big(\ket{0}+\ket{1}\Big)\bra{0} + \Big(\ket{0}-\ket{1}\Big)\bra{1} \bigg) = \frac{1}{\sqrt{2}} \bigg( \ket{0}\bra{0}+\ket{1}\bra{0} + \ket{0}\bra{1}-\ket{1}\bra{1} \bigg)\tag{2.2.2} \end{gather}
which is the Hadamard gate in Dirac notation. Hadamard operation is a rotation of the Block sphere about y axis by \(\frac{\pi}{2}\text{,}\) followed by a rotation about \(x\) axis by \(pi\text{.}\)
Calculate
  • \begin{equation*} H\ket{0} \end{equation*}
  • \begin{equation*} H\ket{1} \end{equation*}
Solution.
  • \begin{equation*} H\ket{0} =\frac{1}{\sqrt{2}} \Big(\ket{0}+\ket{1}\Big) \end{equation*}
  • \begin{equation*} H\ket{1} =\frac{1}{\sqrt{2}} \Big(\ket{0}-\ket{1}\Big) \end{equation*}

Subsection 2.2.2 Pauli X gate

Pauli X gate is also labeled as \(\sigma_1\text{,}\) \(\sigma_x\) or X
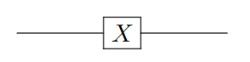
Figure 2.2.3. X gate representation in a circuit.
\begin{align} X= \text{NOT}= \begin{pmatrix} 0&1\\ 1&0 \end{pmatrix}\tag{2.2.3} \end{align}
Calculate
  • \begin{equation*} X\ket{0} \end{equation*}
  • \begin{equation*} X\ket{1} \end{equation*}
  • \begin{equation*} X(X\ket{0}) \end{equation*}
  • \begin{equation*} X(X\ket{1}) \end{equation*}
Solution.
  • \begin{equation*} X\ket{0}=\ket{1} \end{equation*}
  • \begin{equation*} X\ket{1}=\ket{0} \end{equation*}
  • \begin{equation*} X(X\ket{0})=\ket{0} \end{equation*}
  • \begin{equation*} X(X\ket{1})=\ket{1} \end{equation*}

Subsection 2.2.3 Pauli Y gate

Pauli Y gate is also labeled as \(\sigma_2\text{,}\) \(\sigma_y\) or Y
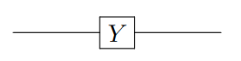
Figure 2.2.5. Y gate representation in a circuit.
\begin{align} Y=\begin{pmatrix} 0&-i\\ i&0 \end{pmatrix}\tag{2.2.4} \end{align}
Calculate
  • \begin{equation*} Y\ket{0} \end{equation*}
  • \begin{equation*} Y\ket{1} \end{equation*}
  • \begin{equation*} Y(Y\ket{0}) \end{equation*}
  • \begin{equation*} Y(Y\ket{1}) \end{equation*}
Solution.
\begin{equation*} Y\ket{0}=i\ket{1} \end{equation*}
\begin{equation*} Y\ket{1}=-i\ket{0} \end{equation*}
\begin{equation*} Y(Y\ket{0})=\ket{0} \end{equation*}
\begin{equation*} Y(Y\ket{1})=\ket{1} \end{equation*}

Subsection 2.2.4 Pauli Z

Pauli Z gate is also labeled as \(\sigma_3\text{,}\) \(\sigma_z\) or Z
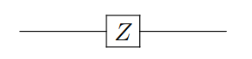
Figure 2.2.7. Z gate representation in a circuit.
\begin{align} Z=\begin{pmatrix} 1&0\\ 0&-1 \end{pmatrix}\tag{2.2.5} \end{align}
Calculate
  • \begin{equation*} Z\ket{0} \end{equation*}
  • \begin{equation*} Z\ket{1} \end{equation*}
  • \begin{equation*} Z(Z\ket{0}) \end{equation*}
  • \begin{equation*} Z(Z\ket{1}) \end{equation*}
Solution.
  • \begin{equation*} Z\ket{0}=\ket{0} \end{equation*}
  • \begin{equation*} Z\ket{1}=-\ket{1} \end{equation*}
  • \begin{equation*} Z(Z\ket{0})=\ket{0} \end{equation*}
  • \begin{equation*} Z(Z\ket{1})=\ket{1} \end{equation*}

Subsection 2.2.5 Pauli I gate

Pauli I gate is also labeled as \(\sigma_0\) or I
Figure 2.2.9. I gate representation in a circuit.
\begin{align} I=\begin{pmatrix} 1&0\\ 0&1 \end{pmatrix}\tag{2.2.6} \end{align}
Calculate
  • \begin{equation*} \sigma_0\ket{0} \end{equation*}
  • \begin{equation*} \sigma_0\ket{1} \end{equation*}
Solution.
  • \begin{equation*} \sigma_0\ket{0}=\ket{0} \end{equation*}
  • \begin{equation*} \sigma_0\ket{1}=\ket{1} \end{equation*}

Subsection 2.2.6 Phase gate

Phase gate is written as S.
Figure 2.2.11. Phase gate representation in a circuit.
\begin{align} S=\begin{pmatrix} 1&0\\ 0&i \end{pmatrix}\tag{2.2.7} \end{align}
Calculate
  • \begin{equation*} S\ket{0} \end{equation*}
  • \begin{equation*} S\ket{1} \end{equation*}
  • \begin{equation*} S(S\ket{0}) \end{equation*}
  • \begin{equation*} S(S\ket{1}) \end{equation*}
Solution.
  • \begin{equation*} S\ket{0}=i\ket{1} \end{equation*}
  • \begin{equation*} S\ket{1}=-i\ket{0} \end{equation*}
  • \begin{equation*} S(S\ket{0})=\ket{0} \end{equation*}
  • \begin{equation*} S(S\ket{1})=-\ket{0} \end{equation*}

Subsection 2.2.7 \(\pi\)/8 gate

\(\pi\)/8 gate is written as T.
Figure 2.2.13. \(\pi\)/8 gate representation in a circuit.
\begin{align} T=\begin{pmatrix} 1&0\\ 0&e^{i\frac{\pi}{4}} \end{pmatrix}\tag{2.2.8} \end{align}
Calculate
  • \begin{equation*} T\ket{0} \end{equation*}
  • \begin{equation*} T\ket{1} \end{equation*}
Solution.
  • \begin{equation*} T\ket{0}=e^{i\frac{\pi}{8}}\ket{0} \end{equation*}
  • \begin{equation*} T\ket{1}=e^{i\frac{\pi}{8}}\ket{1} \end{equation*}
Previous gates aplly on single qubit. The following subsections show the multiqubit gates.

Subsection 2.2.8 Controled-NOT

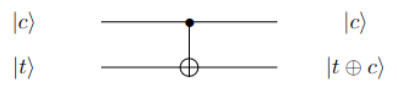
CNOT gate in the quantum context has two input qubits:
  • Control qbit\(\bullet\)
  • target qbit\(\oplus\)
This gate acts as following
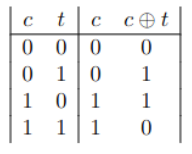
Figure 2.2.15. CNOT gate representation in a circuit.
\begin{gather} \label{eq:CTQbitCNOT} \ket{c}\ket{t}\to \ket{c}\ket{t\oplus c}\tag{2.2.9} \end{gather}
Check the XOR and notice this gate is for two qubits.
Obtain the Dirac notation
  • \(c\to0\) and \(t\to0\)
  • \(c\to0\) and \(t\to1\)
  • \(c\to1\) and \(t\to0\)
  • \(c\to1\) and \(t\to1\)
(\(\ket{00}\) can be written as \(\ket{0,0}\))
Solution.
  • \(\displaystyle \ket{00}\bra{00}\)
  • \(\displaystyle \ket{01}\bra{01}\)
  • \(\displaystyle \ket{10}\bra{11}\)
  • \(\displaystyle \ket{11}\bra{11}\)
The gate and matrix representation are,
Figure 2.2.17. CNOT gate representation in a circuit.
\begin{align} CNOT=\neg X= \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix}\tag{2.2.10} \end{align}
Since
\begin{align} \begin{pmatrix} \ket{00}\bra{00} & \ket{00}\bra{01} & \ket{00}\bra{10} & \ket{00}\bra{11} \\ \ket{01}\bra{00} & \ket{01}\bra{01} & \ket{01}\bra{10} & \ket{01}\bra{11} \\ \ket{10}\bra{00} & \ket{10}\bra{01} & \ket{10}\bra{10} & \ket{10}\bra{11} \\ \ket{11}\bra{00} & \ket{11}\bra{01} & \ket{11}\bra{10} & \ket{11}\bra{11} \end{pmatrix}\tag{2.2.11} \end{align}
and using CNOT matrix we can cancel out some terms and reduce others to 1, such as
\begin{align} \begin{pmatrix} \cancelto{1}{\ket{00}\bra{00}} & \ket{00}\bra{01} & \ket{00}\bra{10} & \ket{00}\bra{11} \\ \ket{01}\bra{00} & \cancelto{1}{\ket{01}\bra{01}} & \ket{01}\bra{10} & \ket{01}\bra{11} \\ \ket{10}\bra{00} & \ket{10}\bra{01} & \ket{10}\bra{10} & \cancelto{1}{\ket{10}\bra{11}} \\ \ket{11}\bra{00} & \ket{11}\bra{01} & \cancelto{1}{\ket{11}\bra{10}} & \ket{11}\bra{11} \end{pmatrix}\tag{2.2.12} \end{align}
and we have
\begin{gather} CX = \ket{00}\bra{00} +\ket{01}\bra{01} +\ket{10}\bra{11} +\ket{11}\bra{10}.\tag{2.2.13} \end{gather}
which is the Dirac representation for the CNOT gate.
Figure 2.2.18. CNOT gate representation in a circuit.
Apply CNOT to the state \(\alpha\ket{10}+\beta\ket{11}\)
Solution.
\((\alpha+\beta)\ket{11}\)

Subsection 2.2.9 Contorolled-U

Let U be a two qbit operation with a control and target qbit. This operation sets the control qbit in order U is applied to the target qbit, otherwise the target qbit is left alone.
\begin{gather} \ket{c}\ket{t}\to \ket{c}U^{c}\ket{t\oplus c}\tag{2.2.14} \end{gather}
This operation is called controlled-U operation represented by
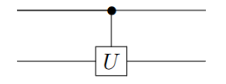
Figure 2.2.20. CU representation in a circuit
CU operator as Dirac notation
\begin{gather} CU\ket{\psi} = \bigg(\ket{0}\bra{0}\otimes I + \ket{1}\bra{1} \otimes U\bigg) \ket{\psi}\tag{2.2.15} \end{gather}

Subsection 2.2.10 Contorolled-Z

The unitary matrix in the computational basis is,
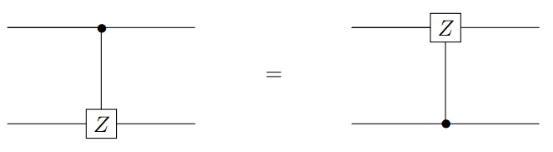
Figure 2.2.21. CZ representation in a circuit
\begin{align} \text{CZ}= \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix}\tag{2.2.16} \end{align}
Obtain
  • \begin{equation*} CZ\ket{00} \end{equation*}
  • \begin{equation*} CZ\ket{01} \end{equation*}
  • \begin{equation*} CZ\ket{10} \end{equation*}
  • \begin{equation*} CZ\ket{11} \end{equation*}
Solution.
  • \begin{equation*} CZ\ket{00}=\ket{00} \end{equation*}
  • \begin{equation*} CZ\ket{01}=\ket{01} \end{equation*}
  • \begin{equation*} CZ\ket{10}=\ket{11} \end{equation*}
  • \begin{equation*} CZ\ket{11}=\ket{11} \end{equation*}
<Prev^TopNext>